Abstract
The Sound Of Fractions is an educational environment for students in middle schools mathematics who have not yet understood fractions as a system of parts and wholes. The interface animates multiple representations in auditory and visual modalities, allowing entries through tapping as well as more standard drag and drop and selection methods. Novel elements of the design mediate between an embodied musical notion of parts and wholes and standard mathematical representations like pies, blocks and number lines, now allowing both complement and contrast in questions.
Introduction
What is like to be a student in the sixth grade and not have learned fractions? It is a painful rehashing of techniques that have not worked for the prior 3 or 4 years, augmented with mind-numbing drill-and-practice computer tools. For these students, a new approach may be more effective – particularly one that speaks to their already familiar understandings and mastered skills. We take a very different approach with “SoundOfFractions”.
Current Mathematical Problems
The current note reports a pedagogically-based design response to that situation. The SoundOfFractions is a microworld [2,3,4,6] to teach 6th graders (10-11 year olds) in a low-performing school who failed their 5th grade, high-stakes mathematics test. They have not yet managed to master the basics of fractions despite years of standard instruction. Their teacher characterized these children as making such systematic mistakes such as adding 1/3 and 1/2 and getting 2/5. Similar problems occur with other systems in arithmetic. They do not understand place value reliably (the notion that the value of a number depends on its position relative to other numbers) and they often cannot carry or borrow.
Interactions
Students interact with each other through guided activities without the use of a computer. These exercises allow the students to express themselves with their own musical expression, and prepares them for the transition in the digital microworld. SoundOfFractions allow the students to tap in and record their own rhythm, and it is automatically converted to a ‘bead’ representation, a novel and powerful representation that allows for consideration of both the part and whole, a required step in full understanding fractions [6]. From this entrance into the microworld, the students can manipulate the rhythm by dragging beats on and off the measure, in addition to toggle the beat on and off.
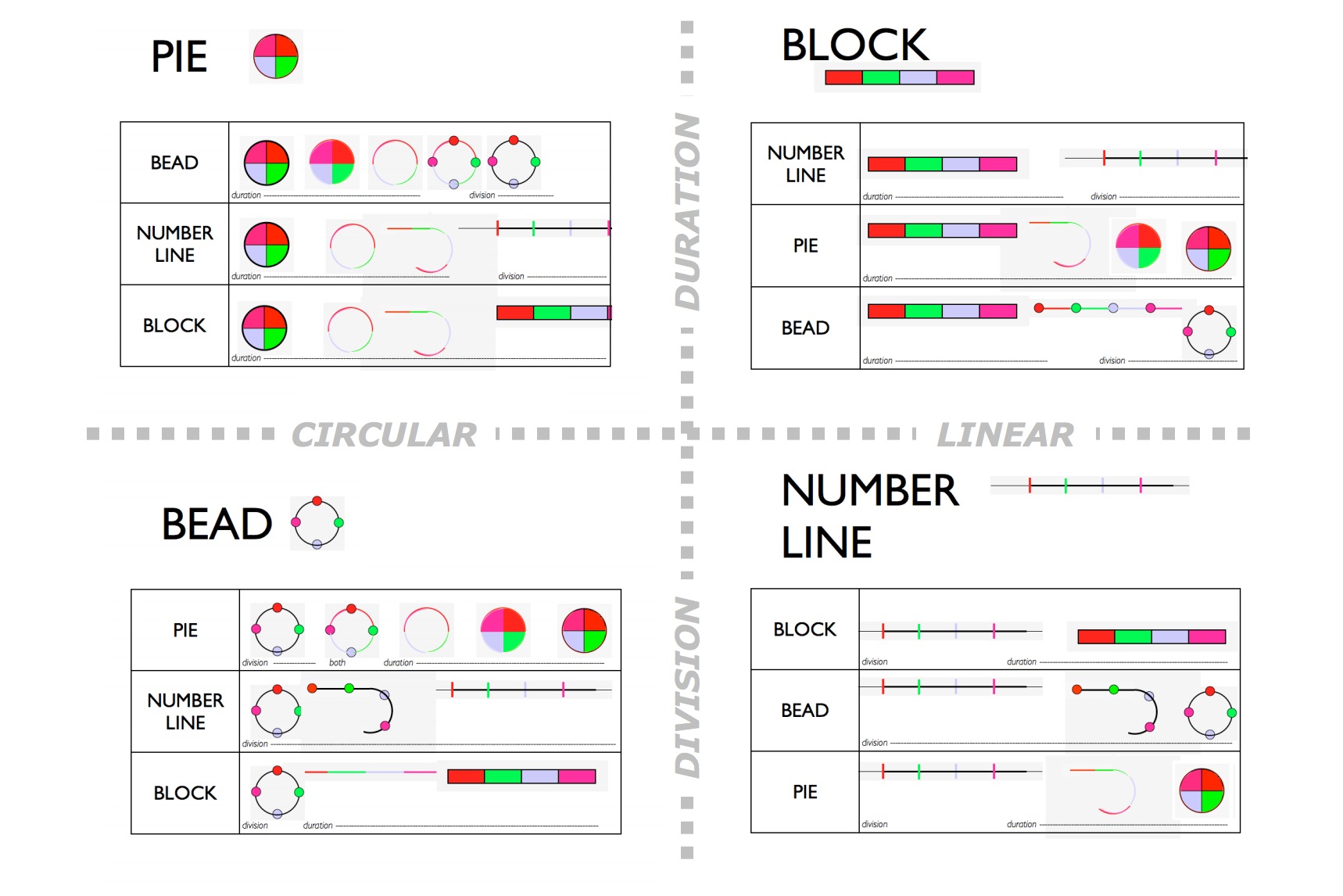
We support multiple percussive instruments, as well as multiple representations of the same rhythm, allowing comparison of representations that highlight the parts (pie and bar), divisions (line and bar), or temporal and embodied (light). A powerful feature of the program is the ability to transform a representation from one to another. This shows conservation of some elements and removal of others. The separation forces the students to use a common mathematical vocabulary to collaborate with other students or to make multiple instruments have complementary rhythms.
Representations and corresponding Transformations
Put simply, understanding fractions requires seeing three things at once: the parts, the whole, and their relationship [6]. The mathematical goal is to see the system. Ultimately the formal mathematical representations follow. The design brief includes addressing both mathematical and social/emotional goals. These students have encountered personal and public failure. It is particularly important (1) to use existing strengths and interests, (2) not to treat them like younger children, (3) not to ask them to use the same materials and approaches that had already proved a problem and (4) not to depend on a pre-existing fondness for fractions or mathematics.
Current Version
SoundOfFractions is hosted at http://compthink.cs.vt.edu:3000/ .
The repository is hosted on Github at https://github.com/VT-CHCI/SoundOfFractions/ .
Team
Institutional Review Board (IRB #14-831):
References
1. Eglash, R. Bennet, A., O’Donnell, C. et al., (2006) Culturally Situated Design Tools: Ethnocomputing from Field Site to Classroom. American Anthropologist. 108(2). 347-362.
2. National Research Council. How People Learn: Brain, Mind, Experience, and School: Expanded Edition. Washington, DC: The National Academies Press, 2000.
3. Papert, S. (1981) Mindstorms. New York: Basic Books.
4. Resnick. M. (1994) Turtles, Termites, and Traffic Jams. Cambridge: MIT Press.
5. Schwartz, D. L. and Bransford, J. D. (1998) A Time for Telling, Cognition & Instruction, 16(4), 475-522.
6. Wilkins, J. L. M., & Norton, A. (2011). The splitting loope. Journal for Research in Mathematics Education, 42(4), 386-406